正弦函數(shù)的單調區(qū)間
正弦函數(shù) \( y = \sin(x) \) 是周期函數(shù),其周期為 \( 2\pi \)。正弦函數(shù)在一個周期內(nèi)有兩個單調遞增區(qū)間和一個單調遞減區(qū)間。
1. 單調遞增區(qū)間:正弦函數(shù)在每個周期的前半段是單調遞增的,即從 \( 0 \) 到 \( \pi \)。具體來說,正弦函數(shù)在區(qū)間 \( [0, \pi]\) 上單調遞增。
2. 單調遞減區(qū)間:正弦函數(shù)在每個周期的后半段是單調遞減的,即從 \( \pi \) 到 \( 2\pi \)。具體來說,正弦函數(shù)在區(qū)間 \( [\pi, 2\pi]\) 上單調遞減。
由于正弦函數(shù)是周期函數(shù),所以其單調性可以擴展到任意整數(shù)倍的周期上。例如,對于任意整數(shù) \( k \),正弦函數(shù)在區(qū)間 \( [2k\pi, (2k+1)\pi]\) 上單調遞增,在區(qū)間 \( [(2k+1)\pi, (2k+2)\pi]\) 上單調遞減。
這些性質可以通過正弦函數(shù)的圖像直觀理解,也可以通過其導數(shù)來數(shù)學證明。正弦函數(shù)的導數(shù)是余弦函數(shù) \( y = \cos(x) \),當余弦函數(shù)的值大于0時,正弦函數(shù)遞增;當余弦函數(shù)的值小于0時,正弦函數(shù)遞減。
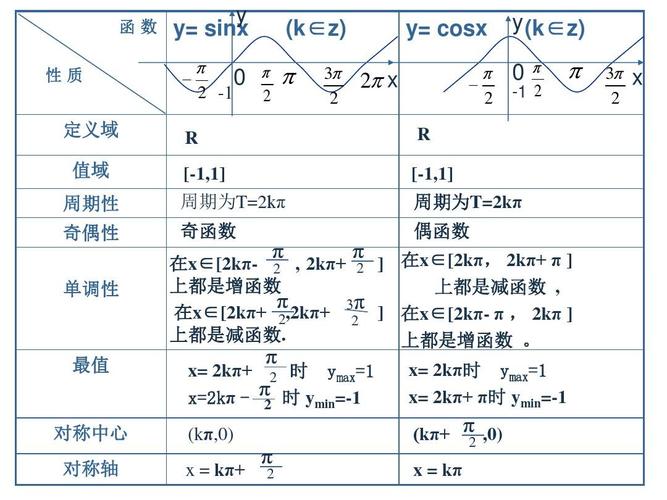
sin和cos的單調遞增遞減區(qū)間
正弦函數(shù) \( \sin(x) \) 和余弦函數(shù) \( \cos(x) \) 都是周期函數(shù),周期為 \( 2\pi \)。它們的單調性在每個周期內(nèi)是重復的。
正弦函數(shù) \( \sin(x) \) 的單調性:
1. 單調遞增區(qū)間:在每個周期內(nèi),正弦函數(shù)從 \( 0 \) 增加到 \( \pi \)(不包括端點),然后從 \( \pi \) 減少到 \( 2\pi \)。所以,對于任意整數(shù) \( k \),單調遞增區(qū)間為:
\[ 2k\pi < x < (2k + 1)\pi \]
2. 單調遞減區(qū)間:正弦函數(shù)從 \( \pi \) 減少到 \( 0 \),然后從 \( 0 \) 增加到 \( 2\pi \)。所以,對于任意整數(shù) \( k \),單調遞減區(qū)間為:
\[ (2k + 1)\pi < x < (2k + 2)\pi \]
余弦函數(shù) \( \cos(x) \) 的單調性:
1. 單調遞增區(qū)間:余弦函數(shù)從 \( 2\pi \) 減少到 \( \pi \),然后從 \( \pi \) 增加到 \( 0 \)。所以,對于任意整數(shù) \( k \),單調遞增區(qū)間為:
\[ (2k + 1)\pi < x < (2k + 2)\pi \]
2. 單調遞減區(qū)間:余弦函數(shù)從 \( 0 \) 減少到 \( \pi \),然后從 \( \pi \) 增加到 \( 2\pi \)。所以,對于任意整數(shù) \( k \),單調遞減區(qū)間為:
\[ 2k\pi < x < (2k + 1)\pi \]
這些區(qū)間描述了正弦和余弦函數(shù)在一個周期內(nèi)的單調性。由于它們是周期函數(shù),這些單調性會在每個 \( 2\pi \) 的周期內(nèi)重復出現(xiàn)。
y=asin(wt+φ)的圖象與性質
函數(shù) \( y = A \sin(\omega t + \phi) \) 是一個正弦函數(shù),其中 \( A \) 是振幅,\( \omega \) 是角頻率,\( t \) 是時間,\( \phi \) 是相位,這個函數(shù)描述了在時間 \( t \) 時刻的正弦波的值。下面是這個函數(shù)圖像的一般性質:
1. 振幅 \( A \):函數(shù)的最大值和最小值分別是 \( A \) 和 \( -A \)。振幅決定了波的高度。
2. 角頻率 \( \omega \):決定了函數(shù)的周期性。周期 \( T \) 可以通過 \( T = \frac{2\pi}{\omega} \) 來計算。角頻率越大,周期越短。
3. 相位 \( \phi \):決定了波的起始點。如果 \( \phi > 0 \),波形會向左移動;如果 \( \phi < 0 \),波形會向右移動。
4. 頻率:是角頻率的倒數(shù)乘以 \( 2\pi \),即 \( f = \frac{\omega}{2\pi} \)。
5. 圖像:正弦函數(shù)的圖像是一條波浪線,它在 \( y = A \) 和 \( y = -A \) 之間振蕩。
6. 奇偶性:正弦函數(shù)是奇函數(shù),即 \( \sin(-x) = -\sin(x) \)。
7. 零點:函數(shù)的零點是 \( t = -\frac{\phi}{\omega} + \frac{2k\pi}{\omega} \),其中 \( k \) 是整數(shù)。
8. 對稱性:正弦函數(shù)是關于其最大值和最小值對稱的,即 \( \sin(\theta) = \sin(\pi - \theta) \)。
9. 相位移動:如果 \( \phi \) 是正值,那么整個波形會沿著時間軸向左平移 \( \phi \) 個單位;如果 \( \phi \) 是負值,則向右平移。
10. 垂直拉伸和壓縮:如果 \( A \) 不等于 1,那么波形會在 \( y \) 軸方向上被拉伸或壓縮。
通過改變振幅 \( A \),角頻率 \( \omega \),和相位 \( \phi \),可以控制正弦波的形狀和位置。這些性質對于理解和分析物理現(xiàn)象,如聲波、電磁波、以及許多其他類型的周期性現(xiàn)象非常重要。

 微信掃一掃打賞
微信掃一掃打賞