數(shù)學(xué)三考研考什么
考研數(shù)學(xué)三主要考察以下三個(gè)部分的內(nèi)容：
1. 微積分：約占試卷的60%，包括函數(shù)、極限、連續(xù)性、一元函數(shù)微積分學(xué)、多元函數(shù)微積分學(xué)、無窮級(jí)數(shù)、常微分方程與差分方程。具體內(nèi)容包括函數(shù)的概念及表示法、數(shù)列極限與函數(shù)極限的定義及其性質(zhì)、導(dǎo)數(shù)和微分的概念、基本初等函數(shù)的導(dǎo)數(shù)、復(fù)合函數(shù)、反函數(shù)和隱函數(shù)的微分法、高階導(dǎo)數(shù)、一階微分形式的不變性、微分中值定理、洛必達(dá)法則、函數(shù)單調(diào)性的判別、函數(shù)的極值、函數(shù)圖形的凹凸性、拐點(diǎn)及漸近線、函數(shù)圖形的描繪、函數(shù)的最大值與最小值等。
2. 線性代數(shù)：約占試卷的20%，包括行列式、矩陣、向量、線性方程組、矩陣的特征值和特征向量、二次型。考生需要理解矩陣的初等變換和初等矩陣及矩陣等價(jià)的概念，理解矩陣的秩的概念，掌握用初等變換求矩陣的逆矩陣和秩的方法，了解分塊矩陣的概念，掌握分塊矩陣的運(yùn)算法則。
3. 概率論與數(shù)理統(tǒng)計(jì)：約占試卷的20%，包括隨機(jī)事件和概率、隨機(jī)變量及其概率分布、隨機(jī)變量的聯(lián)合概率分布、隨機(jī)變量的數(shù)字特征、大數(shù)定律和中心極限定理、數(shù)理統(tǒng)計(jì)的基本概念、參數(shù)估計(jì)、假設(shè)檢驗(yàn)。考生需要理解隨機(jī)變量數(shù)字特征（數(shù)學(xué)期望、方差、標(biāo)準(zhǔn)差、矩、協(xié)方差、相關(guān)系數(shù)）的概念，會(huì)運(yùn)用數(shù)字特征的基本性質(zhì)，并掌握常用分布的數(shù)字特征。
試卷的題型結(jié)構(gòu)包括單項(xiàng)選擇題、填空題和解答題（包括證明題），試卷滿分為150分，考試時(shí)間為180分鐘。考試難度相對(duì)于數(shù)學(xué)一而言較為簡(jiǎn)單，但仍然需要考生具備扎實(shí)的數(shù)學(xué)基礎(chǔ)和良好的邏輯推理能力。
數(shù)三有多難相比于高考
考研數(shù)學(xué)三（數(shù)三）與高考數(shù)學(xué)的難度比較是一個(gè)復(fù)雜的問題，因?yàn)閮烧叩目荚嚹康摹?nèi)容、題型和評(píng)分標(biāo)準(zhǔn)都有所不同。以下是一些關(guān)鍵點(diǎn)的比較：
1. 考試目的：
- 高考數(shù)學(xué)旨在測(cè)試學(xué)生對(duì)高中數(shù)學(xué)知識(shí)的掌握程度，以及解決基礎(chǔ)數(shù)學(xué)問題的能力。
- 考研數(shù)學(xué)三（數(shù)三）則更側(cè)重于測(cè)試學(xué)生對(duì)高等數(shù)學(xué)知識(shí)的理解和應(yīng)用能力，以及解決更復(fù)雜數(shù)學(xué)問題的能力。
2. 考試內(nèi)容：
- 高考數(shù)學(xué)內(nèi)容通常包括代數(shù)、幾何、概率統(tǒng)計(jì)等基礎(chǔ)數(shù)學(xué)知識(shí)。
- 數(shù)三則包括高等數(shù)學(xué)、線性代數(shù)、概率論與數(shù)理統(tǒng)計(jì)等內(nèi)容，這些內(nèi)容在深度和難度上都超過了高考數(shù)學(xué)。
3. 題型和評(píng)分標(biāo)準(zhǔn)：
- 高考數(shù)學(xué)通常包括選擇題、填空題和解答題，評(píng)分標(biāo)準(zhǔn)相對(duì)固定。
- 數(shù)三則可能包括更復(fù)雜的題型，如證明題、應(yīng)用題等，評(píng)分標(biāo)準(zhǔn)可能更加靈活，更注重解題過程和方法。
4. 難度感受：
- 有觀點(diǎn)認(rèn)為數(shù)三在某些年份的難度相對(duì)較高，尤其是在經(jīng)濟(jì)管理類專業(yè)中，由于報(bào)考人數(shù)多，競(jìng)爭(zhēng)大，使得數(shù)三的難度感受增加。
- 另一方面，也有觀點(diǎn)認(rèn)為數(shù)三的難度相對(duì)于數(shù)一而言較為簡(jiǎn)單，但仍然需要學(xué)生具備扎實(shí)的數(shù)學(xué)基礎(chǔ)和良好的解題技巧。
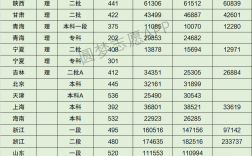
5. 高考難度：
- 高考難度因省份和年份而異，一些省份如河南、廣東等被認(rèn)為是“地獄模式”，而北京、上海等則被認(rèn)為是“優(yōu)惠模式”。
總的來說，考研數(shù)學(xué)三（數(shù)三）在內(nèi)容深度和解題技巧上通常被認(rèn)為比高考數(shù)學(xué)更難，但高考數(shù)學(xué)覆蓋的知識(shí)面更廣，兩者各有側(cè)重點(diǎn)。考生在準(zhǔn)備這兩種考試時(shí)，需要以下是部分真題內(nèi)容及答案解析：
1. 曲線 \( y = e^{x-1} + \frac{1}{e^x} \) 的漸近線方程為 \( y = x + \frac{1}{e} \)。答案為B。
2. 函數(shù) \( f(x) \) 的一個(gè)原函數(shù)為 \( F(x) = \begin{cases} x^2 - \sin(x), & x \leq 0 \\ x^2 + \sin(x), & x > 0 \end{cases} \)。答案為D。
3. 設(shè)數(shù)列 \( \{x_n\} \) 和 \( \{y_n\} \) 滿足 \( x_1 = y_1 = \frac{1}{2} \)，\( x_{n+1} = \sin(x_n) \)，\( y_{n+1} = y_n^2 \)，當(dāng) \( n \to \infty \) 時(shí)，\( y_n \) 是 \( x_n \) 的高階無窮小。答案為B。
4. 已知微分方程 \( y'' + ay' + by = 0 \) 的解在 \( (-\infty, +\infty) \) 上有界，則 \( a = 0 \)，\( b > 0 \)。答案為C。
5. 設(shè)函數(shù) \( y = f(x) \) 由 \( y = \begin{cases} 2x + \sin(t), & t \geq 0 \\ x - t, & t < 0 \end{cases} \) 確定，則 \( f'(0) = 0 \)，\( f''(0) \) 不存在。答案為C。
6. 若函數(shù) \( f(x) = \int_{1}^{x} \frac{\alpha + \ln(t)}{t} \, dt \) 在 \( \alpha = 0 \) 處取得最小值，則 \( \alpha = -\ln(\ln 2) \)。答案為A。
7. 設(shè)函數(shù) \( f(x) = 2(x + a)e^x \)，若 \( f(x) \) 沒有極值點(diǎn)，但曲線 \( y = f(x) \) 有拐點(diǎn)，則 \( a \) 的取值范圍為 \( [1, 2) \)。答案為C。
8. 設(shè) \( A \)，\( B \) 為 \( n \) 階可逆矩陣，\( E \) 為 \( n \) 階單位矩陣，\( *M \) 為矩陣 \( M \) 的伴隨矩陣，則 \( \begin{bmatrix} A & E \\ O & B \end{bmatrix}^* = \begin{bmatrix} B & O \\ A & B \end{bmatrix} \)。答案為C。
以上是部分真題及答案解析，完整的真題及答案解析可以通過以下方式獲取：
- 訪問文都考研網(wǎng)查看2023考研數(shù)學(xué)二真題及答案解析
- 訪問新東方在線查看2023年考研數(shù)學(xué)二真題答案及解析（電子版下載）
- 訪問中國(guó)教育在線查看歷年數(shù)學(xué)真題
- 訪問百度文庫(kù)查看2023年考研《數(shù)學(xué)二》真題試卷完整版（文末含答案及解析）
由于內(nèi)容較多，這里只提供了部分真題及答案解析。如需獲取完整版的真題及答案解析，可以訪問上述網(wǎng)站或平臺(tái)。
微信掃一掃打賞
