中級(jí)會(huì)計(jì)插值法怎么計(jì)算

會(huì)計(jì)插值法，也稱為內(nèi)插法，是一種在已知數(shù)據(jù)點(diǎn)的基礎(chǔ)上，通過線性或非線性關(guān)系推算出未知數(shù)據(jù)點(diǎn)數(shù)值的方法。這種方法在財(cái)務(wù)管理、投資決策、風(fēng)險(xiǎn)管理等方面有廣泛應(yīng)用。插值法的基本原理是通過已知數(shù)據(jù)點(diǎn)之間的數(shù)學(xué)關(guān)系來預(yù)測(cè)未知數(shù)據(jù)點(diǎn)的數(shù)值。

在實(shí)際操作中，插值法通常用于計(jì)算資產(chǎn)的價(jià)值、評(píng)估項(xiàng)目的收益率或確定證券的定價(jià)等。它的計(jì)算過程可以分為以下幾個(gè)步驟：

1. 確定已知點(diǎn)：你需要確定兩個(gè)已知的數(shù)據(jù)點(diǎn)，這兩個(gè)點(diǎn)是用于插值計(jì)算的基礎(chǔ)。假設(shè)這兩個(gè)點(diǎn)是A(i1, b1)和B(i2, b2)，其中i代表自變量（如時(shí)間、利率等），b代表因變量（如現(xiàn)值、收益率等）。

2. 建立方程：如果點(diǎn)P(i, b)在已知點(diǎn)A和B確定的直線上，那么可以得到以下比例關(guān)系：(b - b1) / (i - i1) = (b2 - b1) / (i2 - i1)。

3. 解方程：通過上述比例關(guān)系，可以解出未知的自變量i或因變量b。如果已知b，可以解出i；如果已知i，可以解出b。

4. 計(jì)算：將已知數(shù)值代入方程中進(jìn)行計(jì)算，得出未知數(shù)值。

例如，如果已知當(dāng)利率為4%時(shí)，現(xiàn)值為900；當(dāng)利率為5%時(shí)，現(xiàn)值為1100。現(xiàn)在要求當(dāng)現(xiàn)值為1000時(shí)的利率r，可以使用以下公式計(jì)算：

\[ (1100 - 900) / (5\% - 4\%) = (1000 - 900) / (r - 4\%) \]

解這個(gè)方程可以得到r的值。

插值法的優(yōu)點(diǎn)是計(jì)算過程相對(duì)簡(jiǎn)單，可以快速得出近似值，但它也有局限性，比如只適用于已知數(shù)據(jù)點(diǎn)之間的預(yù)測(cè)，對(duì)于超出已知數(shù)據(jù)范圍的預(yù)測(cè)可能不夠準(zhǔn)確。插值法的結(jié)果依賴于已知數(shù)據(jù)點(diǎn)的準(zhǔn)確性和分布情況，如果數(shù)據(jù)點(diǎn)存在誤差或分布不均，可能會(huì)導(dǎo)致預(yù)測(cè)結(jié)果產(chǎn)生偏差 。

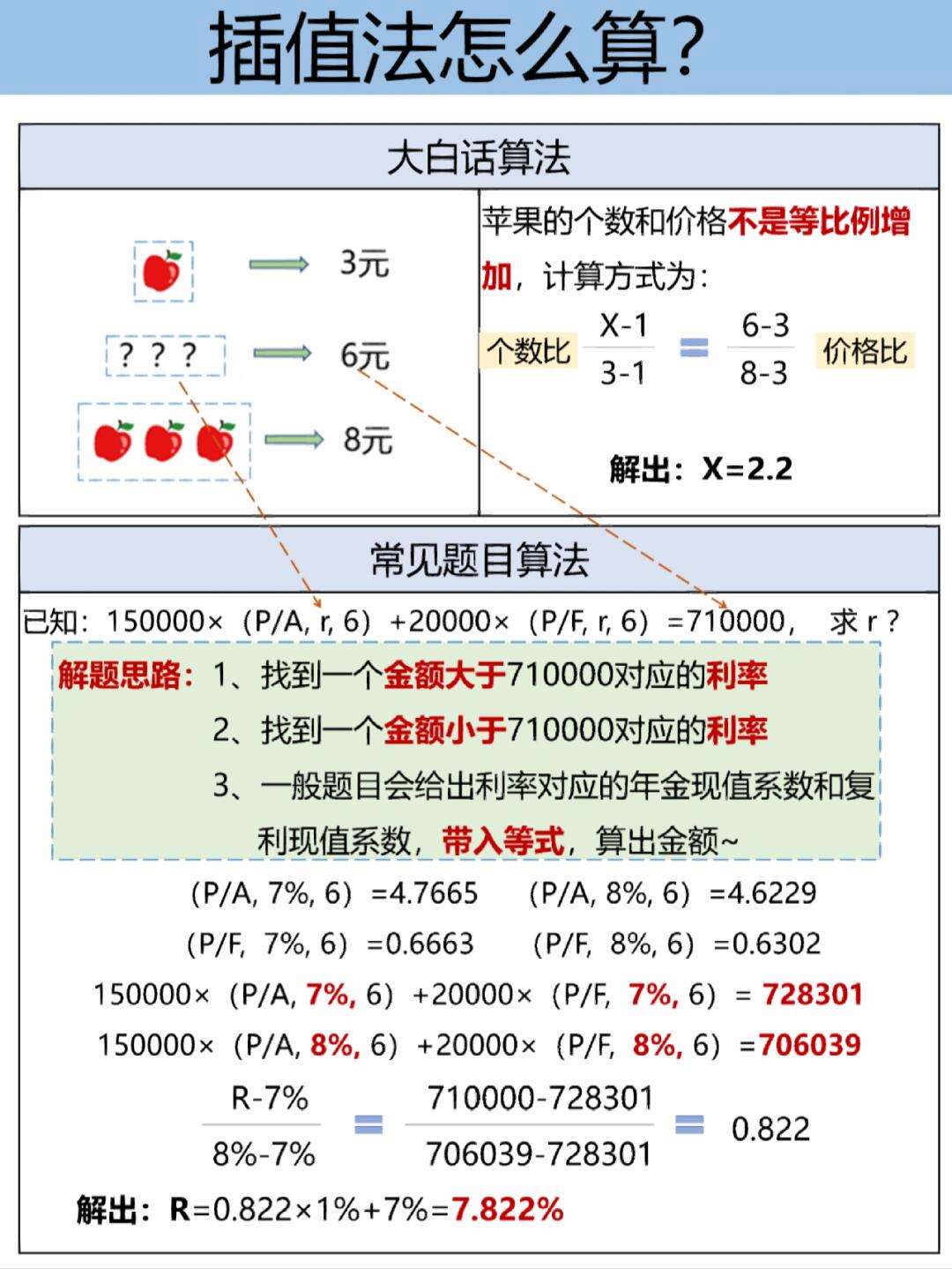
插值法簡(jiǎn)單計(jì)算公式

插值法是數(shù)學(xué)中用于并且 \( x_0 < x < x_1 \)，則線性插值公式為：

\[

y = y_0 + \frac{(y_1 - y_0)}{(x_1 - x_0)} \cdot (x - x_0)

\]

2. 拉格朗日插值：

對(duì)于 \( n+1 \) 個(gè)已知點(diǎn) \( (x_0, y_0), (x_1, y_1), \ldots, (x_n, y_n) \)，拉格朗日插值公式為：

\[

y = \sum_{i=0}^{n} y_i \cdot l_i(x)

\]

其中 \( l_i(x) \) 是拉格朗日基多項(xiàng)式，定義為：

\[

l_i(x) = \prod_{\substack{0 \le j \le n \\ j \ne i}} \frac{x - x_j}{x_i - x_j}

\]

3. 牛頓插值：

牛頓插值公式也是用于 \( n+1 \) 個(gè)已知點(diǎn) \( (x_0, y_0), (x_1, y_1), \ldots, (x_n, y_n) \)，公式為：

\[

y = a_0 + a_1(x - x_0) + a_2(x - x_0)(x - x_1) + \ldots + a_n(x - x_0)(x - x_1) \ldots (x - x_{n-1})

\]

其中 \( a_i \) 是差商。

4. 分段插值：

分段插值是將整個(gè)區(qū)間分成多個(gè)小區(qū)間，然后在每個(gè)小區(qū)間內(nèi)使用一種插值方法（通常是線性或二次插值）。

5. 樣條插值：

樣條插值是分段插值的一種，其中每一段是一個(gè)低階多項(xiàng)式（通常是三次多項(xiàng)式），并且相鄰的多項(xiàng)式在連接點(diǎn)上連續(xù)且光滑。

每種方法都有其適用的場(chǎng)景和優(yōu)缺點(diǎn)。選擇哪種插值方法通常取決于數(shù)據(jù)的特性和所需的精度。

內(nèi)插法和插值法是一樣嗎

內(nèi)插法和插值法通常指的是同一個(gè)概念，它們都是數(shù)學(xué)中用來這兩個(gè)術(shù)語(yǔ)可能會(huì)有所區(qū)別，但基本上它們描述的是相同的過程。

插值法（Interpolation）

插值法是一種數(shù)學(xué)方法，用于構(gòu)造一個(gè)函數(shù)，這個(gè)函數(shù)在一系列已知數(shù)據(jù)點(diǎn)上取已知值。插值的目的是創(chuàng)建一個(gè)平滑的函數(shù)，它能夠通過所有給定的數(shù)據(jù)點(diǎn)，或者至少在這些點(diǎn)上近似地匹配這些值。

內(nèi)插法（Extrapolation）

內(nèi)插法是插值法的一個(gè)特例，它涉及到使用已知數(shù)據(jù)點(diǎn)來估計(jì)這些點(diǎn)之間的未知值。換句話說，內(nèi)插是在已知數(shù)據(jù)點(diǎn)的范圍內(nèi)進(jìn)行估計(jì)。

外插法（Extrapolation）

與內(nèi)插法相對(duì)的是外插法，它涉及到使用已知數(shù)據(jù)點(diǎn)來估計(jì)這些點(diǎn)范圍之外的值。

在實(shí)際應(yīng)用中，內(nèi)插法和插值法通常可以互換使用，尤其是在處理連續(xù)數(shù)據(jù)時(shí)。不過，嚴(yán)格來說，內(nèi)插法是插值法的一個(gè)子集，專門用于已知數(shù)據(jù)點(diǎn)之間的估計(jì)。