專升本高數考試范圍
2024年專升本高等數學考試的范圍主要包括以下幾個部分:
1. 函數與極限:理解函數的概念及表示法;了解函數的有界性、單調性、周期性、奇偶性、反函數、復合函數、隱函數、函數的左右極限、無窮小、無窮大和無窮小與無窮大之間的關系等概念,掌握無窮小的比較和極限的四則運算法則;熟悉極限存在的兩個準則:單調有界準則和夾逼準則;會用兩個重要極限求極限;掌握洛必達(L’Hopsital)法則;了解函數在一點處連續與間斷的概念,會討論函數在一點處的連續性(如分段函數),會判斷間斷點的類型;了解初等函數的連續性,知道閉區間上連續函數的性質(零點定理、介值定理和最大值、最小值定理)。
2. 一元函數微分法及應用:了解導數與微分的概念與關系,理解導數定義求極限;清楚導數的幾何定義和物理意義,會求曲線在一點處的切線方程;了解函數的可導性與連續性之間的關系;熟練掌握導數和微分的運算法則;熟練計算初等函數的一階、二階導數;掌握隱函數和由參數方程確定函數的一階、二階導數的求法;理解羅爾(Rolle)定理,會用羅爾定理討論方程根的問題;掌握判斷函數的單調性和求極值的方法以及討論函數的單調區間;會確定簡單函數圖形的凹凸性和拐點;會利用導數證明簡單不等式;會求解簡單的最大值與最小值問題。
3. 一元函數積分法及應用:理解不定積分的概念及其與原函數的關系;熟練掌握不定積分的基本積分公式和不定積分的換元法與分部積分法;理解定積分的概念,掌握定積分的基本性質(含積分中值定理);了解變上限定積分求導公式,熟練掌握牛頓——萊布尼茲公式;掌握定積分的換元法和分部積分法;了解定積分的元素法,會用定積分求平面圖形面積、旋轉體體積等。
4. 微分方程:能識別可分離變量方程、齊次方程、一階線性方程,并掌握它們的解法;了解二階線性微分方程解的結構;會求二階常系數齊次線性微分方程的通解;會求簡單的二階常系數非齊次線性微分方程的通解(非齊次項為多項式、指數函數及它們的和或乘積)。
5. 向量代數與空間解析幾何:掌握基本的向量運算(線性運算、點積、叉積);掌握平面和直線的方程表達式及其求法;了解平面與平面、平面與直線、直線與直線的平行、垂直的條件和夾角公式,以及點到平面的距離公式。
考試形式為閉卷筆試,試卷滿分為100分,考試時間為120分鐘。題型范圍包括選擇題、填空題和解答題。選擇題主要考察基本概念和基本計算,填空題涉及到的知識點較為廣泛,解答題則注重綜合運用能力和邏輯分析能力的考察。
備考時,建議同學們制定詳細的復習計劃,多做練習題,注重基礎,有條件的話可以參加輔導班。可以參考《高等數學》(第七版)同濟大學應用數學系 高等教育出版社作為參考書目。
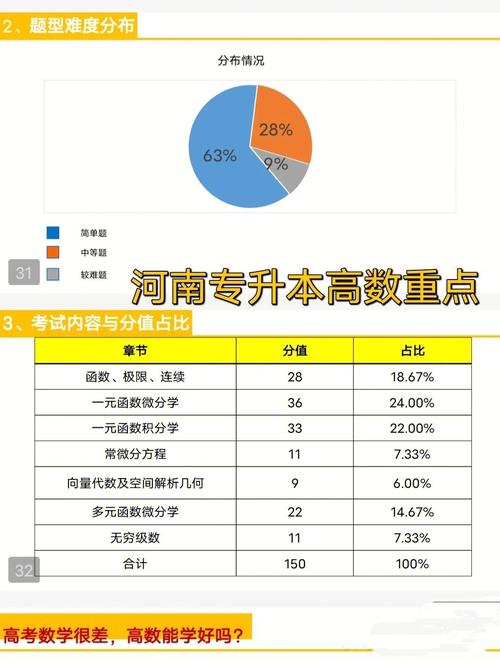
專升本一般多少分穩過
專升本的錄取分數線因地區、院校和專業而異,每年也可能會有所變化。不同專業的最低錄取分數線從80分到236分不等。例如,河南省2024年普通高校專升本招生錄取控制分數線中,經濟學專業為136分,而醫學影像技術專業為184分。廣東省2024年普通專升本招生最低控制分數線中,大學語文為120分/85分,高等數學為105分/60分。
一般來說,統招專升本的錄取分數線文科大約在250—300分,理科大約在170—250分,總分通常為450分。不過,這些數據僅供參考,具體的錄取分數線需要以各省招生主管部門公布的信息為準。考生應該關注所在省份的教育考試院官網或相關院校的招生網站,以獲取最新的專升本錄取分數線信息。
專升本怎么個流程
專升本(專科升本科)的流程通常包括以下幾個步驟:
1. 招生對象:一般包括應屆高職(專科)畢業生、往屆畢業生、退役大學生士兵等。
2. 招生高校及計劃:不同的省份和高校會有不同的招生計劃和專業。
3. 報名:考生需要在規定的時間內登錄指定的報名平臺進行網絡報名,并按照要求提交相關的個人信息和資料。
4. 資格審核:報名結束后,考生需要提交資格審核材料,由招生高校進行審核。
5. 考試:考試通常包括公共課和專業課,具體科目和考試時間會提前公布。
6. 成績公布:考試結束后,成績會在指定的時間公布。
7. 志愿填報:考生招生高校進行錄取。
9. 入學:被錄取的考生按照錄取通知書的要求辦理入學手續。
10. 培養:專升本學生入學后,按照本科教學計劃進行學習。
11. 畢業:完成本科學習后,符合畢業條件的學生可以獲得本科畢業證書。
每個省份的具體流程和時間可能會有所不同,建議考生關注當地教育考試院或招生高校發布的最新通知。

 微信掃一掃打賞
微信掃一掃打賞