1的無窮次方為什么是e
在數學中,\( e \) 是一個非常重要的常數,它約等于 2.71828。\( e \) 通常被稱為自然對數的底數,它在許多數學領域和自然現象中都有出現。
1 的無窮次方等于 \( e \) 這個說法,實際上是一個數學上的近似表達。更準確的表述是,當指數趨向于無窮大時,\( (1 + \frac{1}{n})^n \) 這個表達式的極限是 \( e \)。這里的 \( n \) 是一個正整數,當 \( n \) 趨向于無窮大時,\( \frac{1}{n} \) 趨向于 0,而整個表達式趨向于 \( e \)。
這個極限可以通過多種方式來證明,其中一種方法是使用洛必達法則(L'H?pital's Rule)來解決“0/0”的不定形極限問題:
\[
\lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n = \lim_{n \to \infty} e^{\ln\left(\left(1 + \frac{1}{n}\right)^n\right)} = e^{\lim_{n \to \infty} \frac{n}{n+1}}
\]
由于 \( \frac{n}{n+1} \) 當 \( n \) 趨向于無窮大時趨向于 1,所以:
\[
\lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n = e^1 = e
\]
這個結果表明,隨著 \( n \) 的增加,\( (1 + \frac{1}{n})^n \) 越來越接近 \( e \)。這也是為什么在數學和科學中,\( e \) 被廣泛使用的原因之一。
為什么e的無窮次方不存在
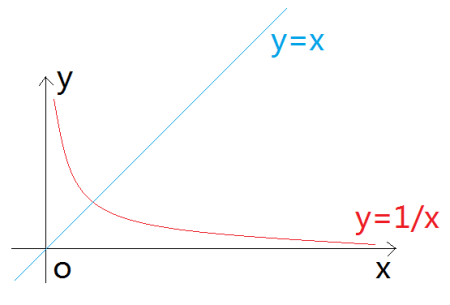
實際上,\(e\) 的無窮次方是存在的,并且是一個非常重要的數學常數,稱為歐拉數 \(e\) 的指數增長。在數學中,\(e\) 被定義為自然對數的底數,其值大約是 2.71828。當指數為無窮大時,\(e\) 的無窮次方表示為 \(e^{\infty}\)。
在數學分析中,指數函數 \(e^x\) 隨著 \(x\) 的增加而無限增長。當 \(x\) 趨向于無窮大時,\(e^x\) 也趨向于無窮大。\(e^{\infty}\) 通常被認為是一個表示趨向于無窮大的符號,而不是一個具體的數值。
在某些數學文獻中,\(e^{\infty}\) 被用來表示一個趨向于無窮大的極限過程,而不是一個具體的數值。這種表示方法有助于簡化某些數學表達式和理論分析。
總之,\(e\) 的無窮次方是存在的,并且是一個無限增長的過程,而不是一個具體的數值。這種概念在數學分析和理論物理等領域有著廣泛的應用。
1的無窮次方是1還是e
\[1\] 的任何正整數次方都是 \[1\],因為任何數除以自身都等于 \[1\]。所以,\[1\] 的無窮次方也是 \[1\]。
\[ e \] 是自然對數的底數,大約等于 \(2.71828\),它與 \(1\) 的無窮次方是兩個完全不同的數學概念。

 微信掃一掃打賞
微信掃一掃打賞