泰勒展開式
泰勒展開式(Taylor series)是數(shù)學(xué)中一種將一個(gè)在某點(diǎn)可導(dǎo)的無窮次函數(shù)用該點(diǎn)處的導(dǎo)數(shù)值構(gòu)建的無窮級數(shù)來近似的方法。泰勒展開式是微積分學(xué)中的一個(gè)重要工具,它允許我們將一個(gè)復(fù)雜的函數(shù)近似為多項(xiàng)式函數(shù),從而簡化計(jì)算。
泰勒展開式的一般形式是:
\[ f(x) = f(a) + f'(a)(x-a) + \frac{f''(a)}{2!}(x-a)^2 + \frac{f'''(a)}{3!}(x-a)^3 + \cdots + \frac{f^{(n)}(a)}{n!}(x-a)^n + R_n(x) \]
其中:
- \( f(x) \) 是要展開的函數(shù)。
- \( a \) 是展開點(diǎn)。
- \( f^{(n)}(a) \) 表示函數(shù)在 \( a \) 點(diǎn)的第 \( n \) 階導(dǎo)數(shù)。
- \( n! \) 表示 \( n \) 的階乘,即 \( n! = n \times (n-1) \times \cdots \times 2 \times 1 \)。
- \( (x-a)^n \) 表示 \( (x-a) \) 的 \( n \) 次冪。
- \( R_n(x) \) 是余項(xiàng),表示 \( n \) 階展開后的誤差。
如果函數(shù) \( f(x) \) 在 \( a \) 點(diǎn)無窮可導(dǎo),那么當(dāng) \( n \) 趨向于無窮大時(shí),余項(xiàng) \( R_n(x) \) 將趨向于 0,泰勒級數(shù)將完全等于原函數(shù)。
一些常見函數(shù)的泰勒展開式:
1. \( e^x \) 在 \( x = 0 \) 處的展開式:
\[ e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots \]
2. \( \sin x \) 在 \( x = 0 \) 處的展開式:
\[ \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots \]
3. \( \cos x \) 在 \( x = 0 \) 處的展開式:
\[ \cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \cdots \]
4. \( \ln(1+x) \) 在 \( x = 0 \) 處的展開式:
\[ \ln(1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \cdots \]
泰勒展開式在物理學(xué)、工程學(xué)、經(jīng)濟(jì)學(xué)等領(lǐng)域都有廣泛的應(yīng)用,比如在物理學(xué)中用于近似計(jì)算復(fù)雜函數(shù)的值,或者在經(jīng)濟(jì)學(xué)中用于近似求解最優(yōu)化問題。
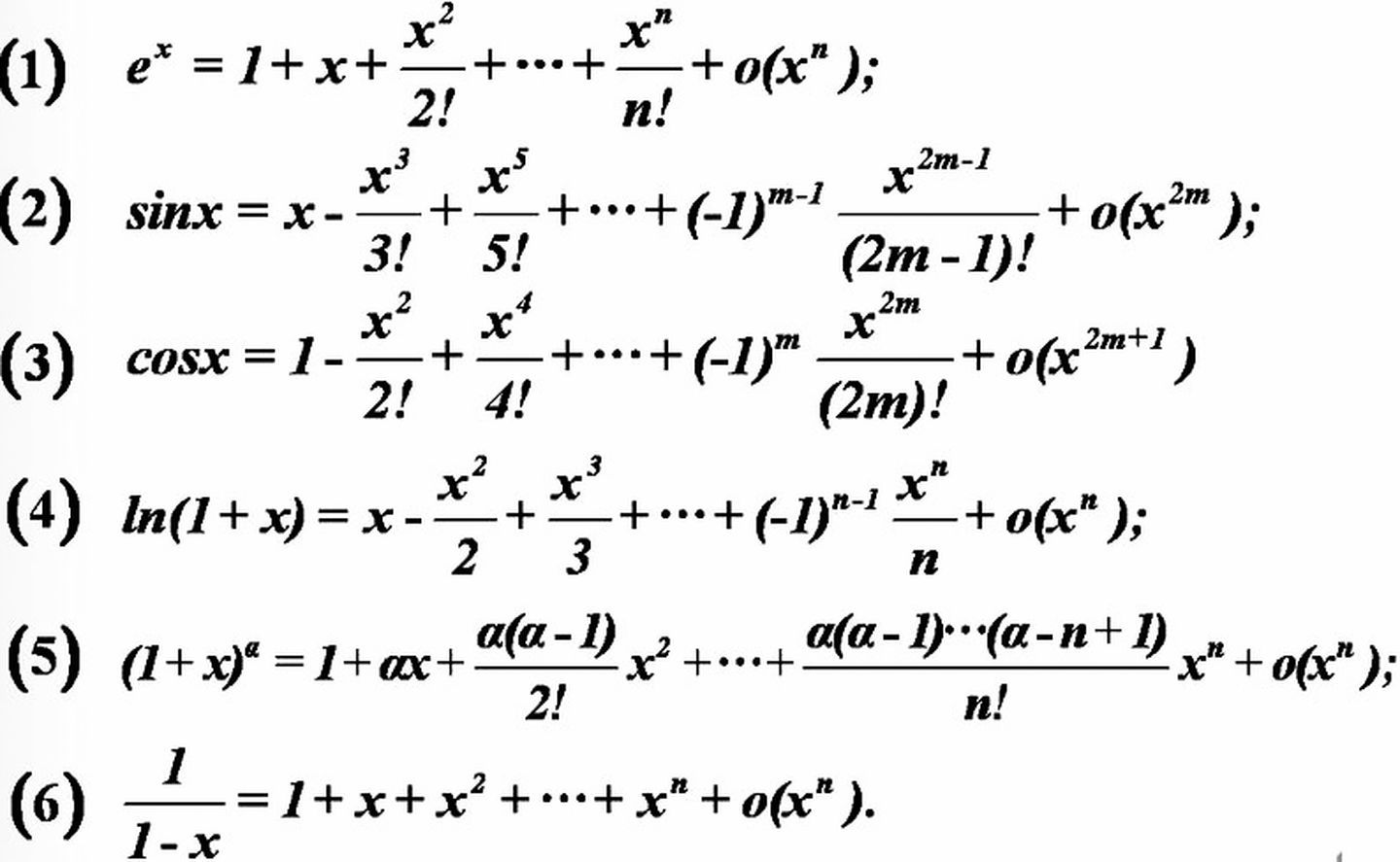
泰勒展開式的推導(dǎo)過程
泰勒展開式(Taylor series)是數(shù)學(xué)中一種將函數(shù)表示為無限級數(shù)的方法。它以函數(shù)在某一點(diǎn)的導(dǎo)數(shù)值為基礎(chǔ),構(gòu)建一個(gè)多項(xiàng)式來近似表示函數(shù)。泰勒展開式在物理學(xué)、工程學(xué)、計(jì)算機(jī)科學(xué)等領(lǐng)域有著廣泛的應(yīng)用。
泰勒展開式的推導(dǎo)過程可以概括為以下幾個(gè)步驟:
1. 函數(shù)在某點(diǎn)的值:我們考慮一個(gè)在點(diǎn) \( a \) 處具有所有階導(dǎo)數(shù)的函數(shù) \( f(x) \)。
2. 函數(shù)增量:考慮函數(shù)在 \( x \) 點(diǎn)的值與在 \( a \) 點(diǎn)的值之間的增量 \( f(x) - f(a) \)。
3. 一階泰勒展開:將增量展開為一階導(dǎo)數(shù)的形式,即:
\[
f(x) - f(a) = f'(a)(x - a) + \frac{f''(a)}{2!}(x - a)^2 + \cdots + \frac{f^{(n)}(a)}{n!}(x - a)^n + R_n(x)
\]
其中,\( R_n(x) \) 是余項(xiàng),表示 \( n \) 階泰勒多項(xiàng)式與原函數(shù)之間的誤差。
4. 泰勒多項(xiàng)式:將上述展開式中的 \( f(a) \) 加回來,得到 \( x \) 點(diǎn)的泰勒多項(xiàng)式:
\[
P_n(x) = f(a) + f'(a)(x - a) + \frac{f''(a)}{2!}(x - a)^2 + \cdots + \frac{f^{(n)}(a)}{n!}(x - a)^n
\]
5. 余項(xiàng):余項(xiàng) \( R_n(x) \) 描述了 \( n \) 階泰勒多項(xiàng)式與原函數(shù)之間的誤差。它可以表示為:
\[
R_n(x) = \frac{f^{(n+1)}(c)}{(n+1)!}(x - a)^{n+1}
\]
其中 \( c \) 是 \( a \) 和 \( x \) 之間的某個(gè)點(diǎn)。
6. 泰勒級數(shù):當(dāng) \( n \) 趨向于無窮大時(shí),如果余項(xiàng) \( R_n(x) \) 趨向于零,那么泰勒多項(xiàng)式就趨向于原函數(shù),這時(shí)的級數(shù)稱為泰勒級數(shù):
\[
f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!}(x - a)^n
\]
泰勒展開式的一個(gè)重要特性是它允許我們將復(fù)雜的函數(shù)近似為多項(xiàng)式,這在數(shù)值計(jì)算和函數(shù)逼近中非常有用。不過,需要注意的是,并不是所有的函數(shù)都可以在所有點(diǎn)上進(jìn)行泰勒展開,且展開式可能只在某個(gè)區(qū)間內(nèi)收斂。
泰勒展開公式使用條件
泰勒展開公式是數(shù)學(xué)分析中的一個(gè)重要工具,它允許我們將一個(gè)在某點(diǎn)可導(dǎo)的函數(shù)展開為無窮級數(shù)的形式。泰勒展開公式的使用條件通常包括以下幾點(diǎn):
1. 可導(dǎo)性:函數(shù)在展開點(diǎn)附近必須足夠可導(dǎo)。對于泰勒級數(shù),至少需要函數(shù)在展開點(diǎn)處可導(dǎo)到所需的階數(shù)。
2. 收斂性:泰勒級數(shù)必須在某個(gè)區(qū)間內(nèi)收斂。對于泰勒級數(shù)的收斂性,通常需要函數(shù)在展開點(diǎn)附近滿足一定的增長條件。
3. 展開點(diǎn):泰勒級數(shù)通常在某個(gè)特定的點(diǎn)(通常是0,稱為麥克勞林級數(shù))展開,但也可以圍繞其他點(diǎn)展開。
4. 余項(xiàng)估計(jì):在實(shí)際應(yīng)用中,我們通常只能計(jì)算有限項(xiàng)的泰勒級數(shù),因此需要對余項(xiàng)(即級數(shù)與函數(shù)之間的誤差)進(jìn)行估計(jì)。常見的余項(xiàng)估計(jì)形式包括拉格朗日余項(xiàng)、柯西余項(xiàng)等。
5. 函數(shù)的光滑性:函數(shù)在展開點(diǎn)附近的光滑性越高(即可導(dǎo)階數(shù)越高),泰勒展開的精度通常越好。
6. 區(qū)間的確定性:泰勒級數(shù)的收斂區(qū)間需要明確,這通常涉及到函數(shù)的性質(zhì)和泰勒級數(shù)的收斂半徑。
7. 解析性:在某些情況下,函數(shù)需要在展開點(diǎn)的某個(gè)鄰域內(nèi)解析(即可以展開為泰勒級數(shù)),這是泰勒級數(shù)收斂的必要條件。
泰勒展開公式的形式通常為:
\[ f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!} (x-a)^n \]
其中,\( f^{(n)}(a) \) 表示函數(shù) \( f \) 在點(diǎn) \( a \) 的第 \( n \) 階導(dǎo)數(shù),\( n! \) 是 \( n \) 的階乘。
在實(shí)際應(yīng)用中,我們通常只計(jì)算有限項(xiàng)的泰勒級數(shù),因此需要根據(jù)具體情況選擇合適的展開點(diǎn)和計(jì)算的項(xiàng)數(shù)。

 微信掃一掃打賞
微信掃一掃打賞