tanx不定積分
\[ \tan(x) \] 的不定積分，即求 \( \int \tan(x) \, dx \)，可以通過對(duì)數(shù)函數(shù)來求解。具體來說，我們可以使用以下積分公式：
\[ \int \tan(x) \, dx = \ln|\cos(x)| + C \]
這里的 \( C \) 是積分常數(shù)。這個(gè)積分的推導(dǎo)涉及到對(duì) \( \tan(x) \) 的表達(dá)式進(jìn)行變換，然后使用基本的積分技巧來求解。如果你需要更詳細(xì)的推導(dǎo)過程或者有其他數(shù)學(xué)問題，隨時(shí)可以問我。
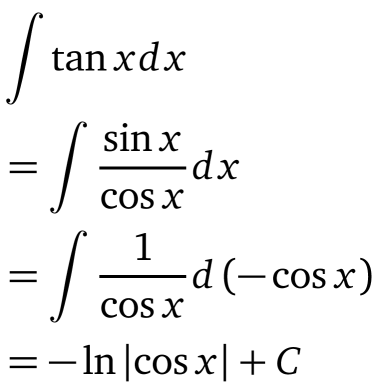
∫tantdt等于什么
積分 \(\int \tan(t) \, dt\) 可以通過對(duì)正切函數(shù)的積分來求解。正切函數(shù) \(\tan(t)\) 可以寫作正弦函數(shù)和余弦函數(shù)的比值，即 \(\tan(t) = \frac{\sin(t)}{\cos(t)}\)。積分 \(\int \tan(t) \, dt\) 的過程如下：
1. 將 \(\tan(t)\) 寫為 \(\frac{\sin(t)}{\cos(t)}\)。
2. 應(yīng)用對(duì)數(shù)函數(shù)的積分規(guī)則，即 \(\int \frac{1}{x} \, dx = \ln|x| + C\)，其中 \(C\) 是積分常數(shù)。
積分過程如下：
\[
\int \tan(t) \, dt = \int \frac{\sin(t)}{\cos(t)} \, dt
\]
由于 \(\sin(t)\) 的積分是 \(-\cos(t)\)，我們可以將 \(\cos(t)\) 看作是 \(\sin(t)\) 的導(dǎo)數(shù)的倒數(shù)，這樣我們可以使用對(duì)數(shù)的積分規(guī)則：
\[
\int \frac{\sin(t)}{\cos(t)} \, dt = \ln|\cos(t)| + C
\]
原積分的解是：
\[
\int \tan(t) \, dt = -\ln|\cos(t)| + C
\]
∫tanxdx如何解出來
積分 \(\int \tan(x) \, dx\) 可以通過對(duì)數(shù)的微積分來解決。我們知道 \(\tan(x) = \frac{\sin(x)}{\cos(x)}\)。積分可以寫為：
\[
\int \tan(x) \, dx = \int \frac{\sin(x)}{\cos(x)} \, dx
\]
接下來，我們可以使用對(duì)數(shù)的性質(zhì)來解決這個(gè)積分。令 \(u = \cos(x)\)，那么 \(du = -\sin(x) \, dx\)。積分變?yōu)椋?/p>
\[
\int \frac{1}{u} \, du
\]
這是一個(gè)簡單的對(duì)數(shù)積分，解為：
\[
\ln|u| + C = \ln|\cos(x)| + C
\]
其中 \(C\) 是積分常數(shù)。\(\int \tan(x) \, dx\) 的解是：
\[
-\ln|\cos(x)| + C
\]
微信掃一掃打賞
